
Dtronics is turning the free Dexed synth plugin, a DX7 emulation, into a hardware synth
The DT-DX is based on the Raspberry Pi-powered MiniDexed DIY synth

The DT-DX is based on the Raspberry Pi-powered MiniDexed DIY synth
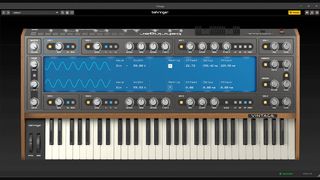
An “accidental leak” was to blame, apparently

“Just don’t blame me - it’s not my fault,” she told the crowd. “Well, it’s partially my fault. But not entirely my fault”

Electronic artist, producer, gear explorer, film composer, and modular master Robin Rimbaud has been releasing music as Scanner and other acts for more than four decades. Here, he gives us a more electronic expert viewpoint on what separates a demo from the finished article…

This all-in-one room correction package means no more excuses for a muddy low-end

Solo artist, collaborator, songwriter, producer, remixer and drummer Georgia Barnes is also a self-confessed synth nerd, which she has every right to blame on her upbringing. Here she explains how she works within that electronic world with producers and artists including Rostam, William Orbit and Olly Alexander…

As their newest soundtrack collaboration, Challengers, gets set for release, the pair break down some of their most iconic work
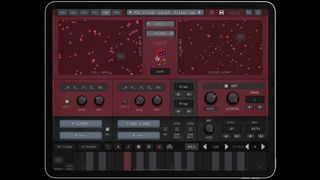
An iOS-based homage to a virtual analogue classic

The Swedish developer launches a sample-based drum machine. We give it a shot

Well, Taylor Swift fans might disagree…

“There is such a magnificent world of ideas and harmonies inside that beautiful head of yours,” she gushes on his 18th birthday

“We are not responsible for the graphics, the sound engine, or anything else related to it”

Synthlation means you can pay nearly six figures for some of these synths (but also get most of their sounds for free)…

Six-track groovebox offers sample and synth engines and step modulation

The Ride frontman chats to Danny Turner about the shoegaze tag and the driving force behind their seventh album, Interplay

Those hoping for the full V Collection experience in hardware form might be disappointed. But, as we discover, AstroLab’s simplicity is its biggest selling point

Master your modular percussion patches

It’s yours for nothing… if the page you’re looking for can ever be found

Headphones designed for both recording and mixing? We're intrigued

Two decades after first starting, Jonnie Wilkes and James Savage finally release their debut Naum Gabo LP, F. Lux. Danny Turner learns more